이번 포스팅에서는 Feature Selection(차원 선택)에 대해 살펴 보겠습니다. 변수를 제거한다고 해서 Feature removal이라고도 합니다. 해당 도메인의 비즈니스를 잘 알면 분석가의 감으로 변수 선택도 가능할 것입니다. 그러나 특성이 너무 많을 경우는 기계적인 방법이 필요합니다. 예를 들어, 자동자 회사에서 부품, 센서 등의 정보들은 정말 많습니다.
Feature selection이란
Feature selection은 간단하게 말하면, 우리가 수집한 dataset의 속성(feature) 중에 예측하고자 하는 target 값의 기여를 많이하는 속성을 선택하는 작업입니다. 속성을 무작위로 선택할 수는 없기 때문에 머신러닝에서는 Filter method, Wrapper method, Embedded method 총 3가지 방법을 사용하고 있습니다.
Filter는 단순히 속성간의 중요도로 변수를 선택하는 방법이고 Wrapper, Embedded는 모델을 만들어 평가하는 방식입니다. Wrapper와 Embedded의 차이는 Wrapper는 변수평가 모델을 이용하여 선택 후 수행하고, Embedded는 수행까지 한 결과로 평가하는 차이가 있습니다.
Filter Method
전처리 단계에서 통계기법을 사용하여 변수 채택하는 방법입니다. 높은 상관계수(영향력)의 feature를 사용하게 됩니다. 여기서 변수 중요도나 상관도에 관련 알고리즘은 다음과 같습니다.
Wrapper Method
Wrapper method는 예측 정확도 측면에서 가장 좋은 성능을 보이는 Feature subset(피처 집합)을 뽑아내는 방법입니다.
변수선택 평가모델은 아래와 같습니다.
- Akaike Information Criteria (AIC)
- Bayesian Information Criteria (BIC)
- 수정R-제곱합(adjusted R-squared)
아무래도 여러 번 Machine Learning을 진행하기 때문에 시간과 비용이 매우 높게 발생합니다. 최종적으로 Best Feature Subset을 찾는 원리이기 때문에 모델의 정확도를 위해 매우 바람직한 방법입니다. feature를 선택하는 방법에 따라 아래 세가지 방법을 사용합니다.
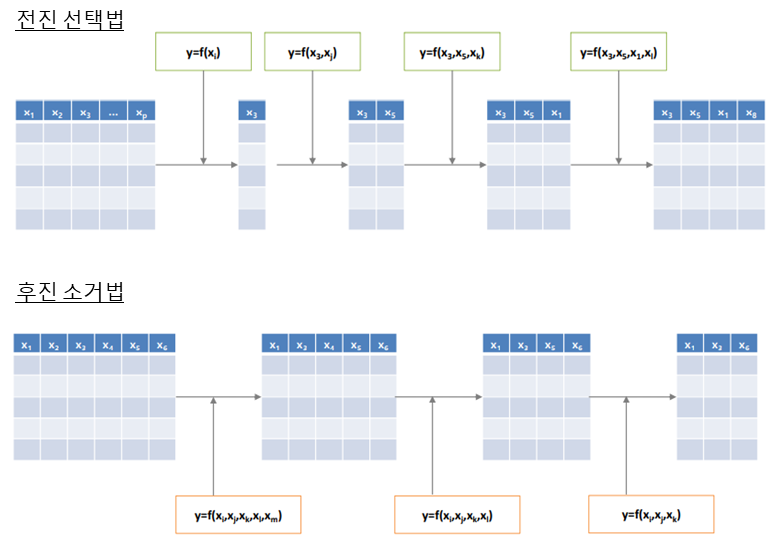
- Forward Selection(전진 선택법) : 변수가 없는 상태로 시작하며, 반복할 때마다 가장 중요한 변수를 추가하여 성능이 가장 좋을 때까지 추가
- Backward Elimination(후진 소거법) : 모든 변수를 가지고 시작하며, 가장 덜 중요한 변수를 하나씩 제거 더 이상 성능의 향상이 없을 때까지 반복
- Stepwise Selection(단계별 선택법) : 설명변수가 하나도 없는 모델에서부터 시작하여 전진선택법과 후진소거법을 번갈아가며 수행함, 가장 시간을 오래 걸리다 보다 우수한 예측 성능을 나타내는 변수 집합을 찾아낼 가능성이 높음
Embedded Method
Embedded method는 Filtering과 Wrapper의 장점을 결합한 방법입니다. 각각의 Feature를 직접 학습하며, 모델의 정확도에 기여하는 Feature를 선택합니다. 계수가 0이 아닌 Feature가 선택되어, 더 낮은 복잡성으로 모델을 훈련하며, 학습 절차를 최적화하는 방식입니다. Lasso, Ridge, Elastic Net 등 규제항을 추가하여 일반화할 수 있습니다.
이렇게 Feature selection에 대해 살펴 보았습니다. 만약 차원 축소 중에 Feature Extraction에 해당하는 PCA 대해 더 알고 싶다면 아래 글에서 참고할 수 있습니다.
차원 축소 - PCA(주성분 분석), Explained Variance Ratio
이번 포스팅에서는 주성분 분석(PCA)에 대해 알아보도록 하겠습니다. 주성분 분석은 차원 축소 방법 중에 가장 많이 사용되는 기법입니다. 그만큼 필수적으로 알아야 할 알고리즘 입니다. PCA(주
bommbom.tistory.com
'데이터 분석' 카테고리의 다른 글
| 차원 축소 - PCA(주성분 분석), Explained Variance Ratio (1) | 2023.10.10 |
|---|---|
| 차원축소 - 투영과 매니폴드(manifold) 학습은 어떻게 다른가? (0) | 2023.10.10 |
| [머신러닝] 차원 축소(Dimensionality Reduction) 이유 및 방법 (1) | 2023.10.06 |
| Boosting 알고리즘 - CatBoost 특징(Ordered Boosting, Target Encoding 장단점) (0) | 2023.10.05 |
| Boosting 알고리즘 - Light GBM 특징(GOSS, EFB, 장단점) (2) | 2023.10.04 |



