이번 포스팅에서는 과적합을 해소하는 방법 중에 정규화에 대해 알아보도록 하겠습니다. 정규화는 제약 조건을 늘려서 모델을 일반화하기 때문에 규제화(Regularization) 라고 부르기도 합니다. 일반적으로 모델의 가중치(weight)에 대한 제약 조건을 추가함으로써 모형이 과도하게 최적화되는 현상을 방지합니다. 즉, 과하게 최적화되는 것을 막는 방법이라고 생각할 수 있습니다. 대표적인 정규화 방법은 라쏘(Lasso)와 릿지(Ridge)가 있습니다.
라쏘(Lasso)
라쏘는 선형 모형에서 쓰이는 MSE 손실함수 = $ \frac{1}{n}\sum (y_{i}-y_{i})^{2} $ 를 사용합니다. 실제 값($ 𝑦_{𝑖} $)과 예측 값($𝑦_{e}$)의 차이가 오차이고, 이 값을 제곱해서 평균 낸 것입니다. 일반적인 선형 모형은 $ y=wx+b $ 의 오차를 최소화 파라미터 w, b를 찾아가게 됩니다. 하지만 훈련용 데이터의 오차만을 최소화하면 과적합이 발생하므로 λ∑|w| 항을 추가합니다. 여기서 λ는 하이퍼파라미터 입니다.
$$ Lasso = \frac{1}{n}\sum (y_{i}-y_{i})^{2} + λ \sum |w| $$
이 수식에서 가중치(w)를 0에 가깝거나 0이 되게 해야 합니다. 이 방법을 통해 모델을 일반화는 1차적인 목적 외에 또 다른 이점은 Feature Selection이 자동으로 이루진다는 것입니다.
릿지(Ridge)
이제 우리는 라쏘를 알고 있습니다. 릿지는 라쏘와 거의 비슷합니다. 다만 정규화 항에 파라미터의 절대값 대신 제곱을 사용한다는 점만 다릅니다.
$$ Ridge = \frac{1}{n}\sum (y_{i}-y_{i})^{2} + λ \sum |w|^{2} $$
규제 항을 확인해 보면 라쏘는 1승, 릿지는 2승을 하는 수식입니다. 그래서 이 두 모형은 각각 L1, L2 정규화라고 부르기도 합니다. 그리고 L1, L2의 이점 모두 가져가기 위해 다 적용하는 모형도 있습니다. 바로 Elastic Net 회귀모형은 가중치의 절대값의 합과 제곱합을 동시에 제약 조건으로 가지는 모형입니다.
라쏘는 Alpha 값을 늘리면 가중치가 0에 가까워지고, 너무 낮추게 되면 규제효과가 없어집니다. 이런 이유 때문에 일반적으로는 분석가들은 릿지를 선호합니다. 그러나 Feature가 많고 그중 일부 Feature만 중요할 경우, 이한 상황에는 라쏘 모형을 선택하기도 합니다.
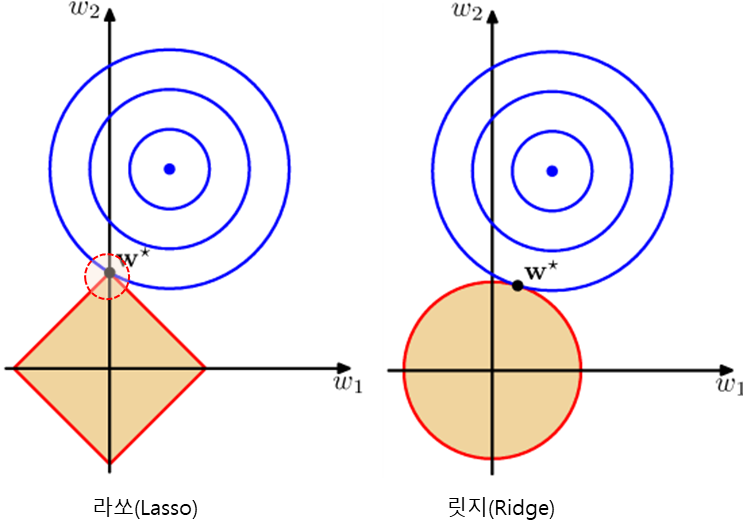
두 도형이 만나는 w∗는 손실함수가 최소화되는 점을 나타냅니다. 라쏘는 0에서 뾰족하게 꺾어지는 형태이기 때문에 손실함수의 최소값이 파라미터가 0인 경우가 많습니다. 그래서 라쏘를 사용하면 파라미터가 0으로 딱 떨어지는 경향이 있습니다. 위의 그림에서도 왼쪽 라쏘의 경우 w∗는 w1=0인 점인 것을 볼 수 있습니다.
분산과 편향
과대적합(overfitting), 과소적합(underfitting)을 이야기하다 보면 분석과 편형이라는 용어가 나옵니다. 분산과 편향은 무엇일까요? Variance(분산)은 모델을 통과한 값들이 서로 얼마나 가까운지를 나타내는 지표입니다. 통계적으로 이야기할 때 데이터가 얼마나 퍼져 있는지를 표현한다고 생각하는 것이 쉽게 이해하는 방법입니다.
Bias(편향)은 모델을 통과한 값이 평균적으로 타깃과 얼마나 차이가 나는지를 나타내는 지표입니다. 실제 예측해야 하는 정답지와 멀어진 정도를 말하며, 단순하게 생각한다면 error와 비슷하게 생각할 수 있습니다. 원하는 정답과 얼마나 벗어났는지에 관한 내용입니다.
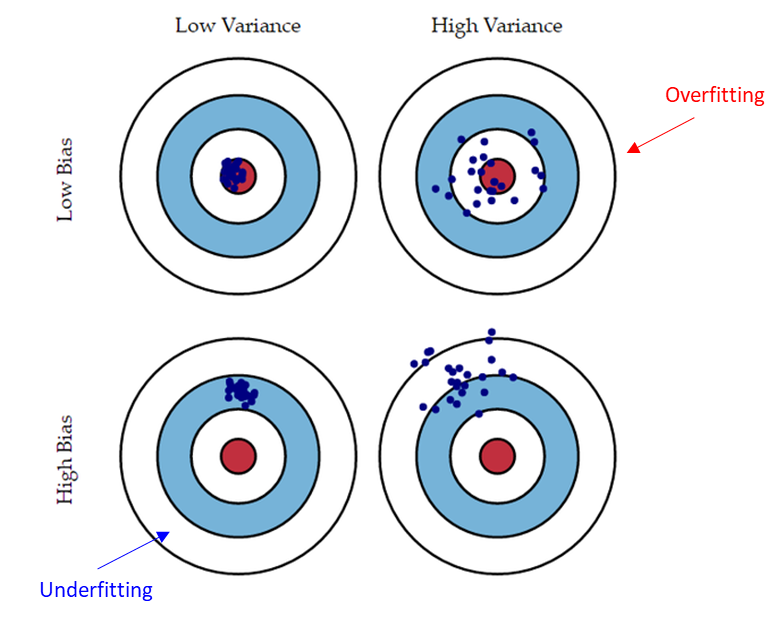
Overfitting/Underfitting과 분산/편향 관계
Overfitting(과대적합)의 경우 예측 값과 타깃의 차이가 작으므로 편향(bias)이 작지만, 모델의 복잡도가 크기 때문에 분산(variance)이 크다고 할 수 있습니다. 새로운 데이터 입력될 경우 분산이 클 가능성이 높습니다.
Overfitting ≒ High variance(분산이 크다)
Underfitting(과소적합)의 경우 모델의 복잡도가 낮아 분산(variance)이 작지만, 훈련 데이터의 적절한 규칙을 찾지 못해 타깃과의 차가 커 편향(bias)이 큽니다. 새로운 데이터 입력될 경우 편향이 클 가능성이 높습니다.
Underfitting ≒ High bias(편향이 크다)
'데이터 분석' 카테고리의 다른 글
| [머신러닝] 선형 회귀 - 옵티마이저와 학습률(Learning Rate) (0) | 2023.09.10 |
|---|---|
| [머신러닝] 선형 회귀(Linear Regression) 와 비용함수 (0) | 2023.09.09 |
| [머신러닝] 과적합(Overfitting) 해소 방법 - 모델 단순화 (0) | 2023.09.07 |
| [머신러닝] 과대적합 vs 과소적합(overfitting, underfitting) (0) | 2023.09.06 |
| [머신러닝] 데이터 전처리 - 변수 결합 (0) | 2023.09.05 |



