이번 포스팅에서는 카이제곱분포에 대해 알아보도록 하겠습니다. 카이제곱 분포는 통계, 특히 가설 검정 및 신뢰 구간 구성의 맥락에서 발생하는 확률 분포입니다. 머신러닝이나 딥러닝에서 카이제곱분포는 속성 선택(feature seletion), 독립성 테스트, 적합도 평가 등에서 일반적으로 사용됩니다.
카이제곱분포란?
나무위키에 따르면 카이제곱분포(chi-squared distribution, χ2 분포)는 n개의 서로 독립적인 표준 정규 확률 변수를 각각 제곱한 다음 합해서 얻어지는 분포라고 설명하고 있습니다. 예전 표현으로 카이자승분포라고 하기도 합니다. 즉 다차원. n차원 확률벡터 y ~ N(0, I)에 대한 분포가 카이제곱분포입니다. 참고로 χ는 그리스 문자 카이(chi)입니다.
좀 더 쉽게 말하면, 여러 개의 정규분포 n개를 독립적으로 추출합니다. 독립적이라는 말은 서로 분포에 영향을 미치지 않는 독립적인 변수의 분포라는 말이죠. 이렇게 n개의 확률분포가 있다면 n개의 변수를 각기 제곱하고 모두 더한 값을 χ2로 정의합니다.(아래 수식 참고)
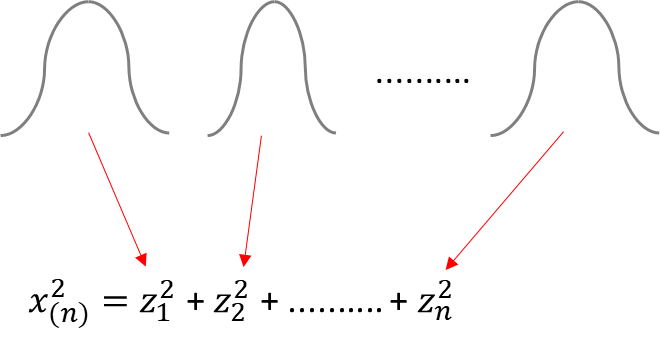
이렇게 카이제곱을 구하는 이유가 무엇일까요?
일반적으루 우리가 푸는 현실 문제는 n차원인 경우가 많습니다. 그런데 이 n차원을 예측 분포와 실제 분포를 비교해야 합니다. 그럴려면 n개의 차원을 합쳐서 분포를 만드는 방법밖에는 없겠죠. 이는 예측된 분포와 실제 분포의 차이를 검증할 수 있다는 이점이 있습니다. 그러면 이런 카이제곱분포를 이용하여 어떤 작업을 할 수 있는지 살펴보도록 하겠습니다.
1. 속성 선택(feature selection)
속성 선택(Feature selection)에서 카이제곱 검정은 범주형 목표(Y) 변수와 각 속성(feature) 간의 독립성을 평가하는 데 자주 사용됩니다. 이 검정(test)은 목표 변수(Y)와 가장 관련성이 높은 feature를 식별하는 데 도움이 됩니다. 카이제곱 검정은 범주형 데이터의 분류 문제에서 속성 선택(Feature Selection)에 적용할 수 있습니다.
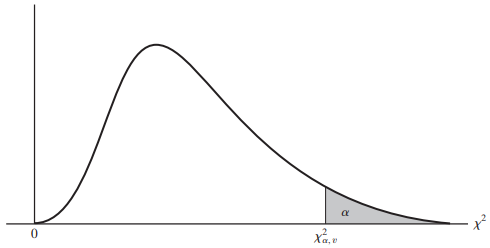
정규분포는 -값과 +값이 존재하지만, 카이제곱분포는 제곱을 하기 때문에 아래와 같이 양수값만 존재합니다. 이 카이제곱 분포에 기초하여 두 범주형 변수(Y변수, X변수) 사이에 유의미한 관계가 있는지를 검정합니다. 두 변수 간의 관계가 많은 속성일 수록 선택하면 됩니다.
2. 독립성 검정(test)
앞에서 설명했듯이 독립성에 대한 카이제곱 검정은 두 범주형 변수 사이에 유의미한 연관성이 있는지 여부를 확인하는 데 사용됩니다. 머신러닝에서 이 테스트를 사용하여 특정 feature의 존재 여부가 다른 feature의 존재 여부와 독립적인지 확인할 수 있습니다. 이 test를 통해 데이터 내의 상관관계를 파악하는 데 사용할 수 있습니다.
3. 적합도
카이제곱 검정은 실제 분포가 예측 분포에 얼마나 잘 맞는지 평가하는 데 사용됩니다. 머신러닝, 딥러닝에서 이는 관찰된 결과와 예상된 결과를 비교하여 모델의 성능을 평가하는 데 유용하게 사용되죠. 예를 들어, 분류 모델의 성능을 평가할 때 적합도에 대한 카이제곱 검정을 사용하여 예측된 클래스 분포를 실제 클래스 분포와 비교할 수 있습니다.
4. 분류의 모델 평가
분류 작업에서는 모델 성능을 평가하기 위해 혼동 행렬(confusion matrix)이 일반적으로 사용됩니다. 카이제곱 통계량은 실제 클래스 빈도와 예측 클래스 빈도 간의 차이가 얼마나 존재하는지 여부를 테스트합니다. 이를 혼동 행렬(confusion matrix)를 통해 계산할 수 있죠. 이는 모델의 전반적인 얼마나 성능이 좋은지를 평가하는 데 도움이 됩니다.
5. 우도비 검정(likelihood rate test)과 불확도 정량화
카이제곱 분포는 다양한 모델에서 관측된 데이터의 우도(likelihood)를 비교하는 우도비 검정에 자주 사용됩니다. 기계 학습에서 우도 비율 테스트는 모델 비교 및 가설 테스트와 같은 영역에 적용할 수 있습니다.
베이지안 통계 및 머신러닝에서 카이제곱 분포는 신뢰할 수 있는 구간을 구성하고 모수 추정치의 불확실성을 정량화하는 구성 요소로도 사용될 수 있습니다.
'데이터 분석' 카테고리의 다른 글
| 커널 함수를 사용하는 이유 (0) | 2024.02.01 |
|---|---|
| Maximum Mean Discrepancy(MMD, 최대 평균 불일치) 개념 정리 (1) | 2024.01.31 |
| 지도학습 비지도학습 쉬운 설명 (0) | 2023.12.18 |
| 머신러닝과 딥러닝의 차이는 무엇일까요? (0) | 2023.11.11 |
| Rule-base 와 머신 러닝은 어떻게 다를까? (6) | 2023.11.08 |



