이번 포스팅은 K-Nearest Neighbor(K-최근접 이웃) 알고리즘에 대해 특징과 학습 방법에 대해 알아보도록 하겠습니다. K-NN은 K-means 알고리즘과 많이 헷갈리는데요. 이번 기회에 정확이 알고 갈 수 있었으면 합니다.
『 '데이널'의 컨텐츠에 포함된 정보는? 』
K-NN의 특징은?
K-means는 비지도 학습이지만 K-NN 알고리즘은 지도학습 입니다. k-means처럼 Clustering 알고리즘이 아닙니다. 이 두 알고리즘을 혼동하기 때문에 시험에 자주 출제됩니다.
K-NN의 아이디어는 유사한 특징을 가진 데이터는 유사한 범주에 속하는 경향이 있다고 가정하는데 부터 시작되었습니다. K-NN 로직을 살펴보면 첫째, 새로운 데이터와 가장 인접한 데이터 k개를 선정합니다. 둘째, k개의 데이터를 이용한 분류 또는 회귀 모델을 생성합니다.
그렇다면 어떻게 인접하다는 것을 알까요? 예상하는 데로 거리 기반으로 알 수 있습니다. 거리를 측정할 때 주로 Euclidian distance를 사용합니다. 그래서 K-NN에서 하이퍼파라미터(hp)는 k값과 '거리 측정 방법' 두 가지입니다.
활율 밀도 추정 알고리즘이라 할 수 있습니다. Sample에 주어진 x에서 가장 가까운 k개의 원소가 많이 속하는 class로 x를 분류하는 비모수적 확률밀도 추정을 하기 때문입니다. K-NN 알고리즘의 활용 분야는 이미지 처리, 이상치 탐지, 영상 속 글자 인식, 얼굴 인식, 암 진단, 개인 선호 예측 및 추천 기술 등에 사용하고 있습니다.
K-NN 알고리즘의 특징을 나타내는 세가지 용어가 있습니다.
- 게으른 학습(Lazy Learner) : 데이터셋만 저장하고 모델을 만들지 않아 게으르다고 표현합니다.
- 사례 기반 학습(Instance-Based Learning) : 과거 사례를 기반으로 계산을 합니다. 이는 학습 모델보다 빠른 예측을 할 수 있습니다.
- 메모리 기반 학습(Memory-Based Learning) : 훈련 데이터로부터 판별 함수(Discriminative Function)를 학습하지 않고, 훈련 데이터 셋을 메모리에 저장하여 사용하는 방법입니다.
학습방법의 차이에 따른 분류
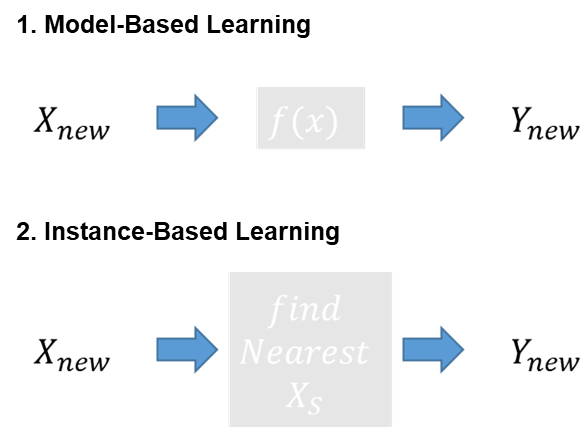
- 모델 기반 학습(Model-Based Learning) : 데이터로 모델을 생성하여 분류 및 예측 진행 합니다. 예를 들어, Linear regression, logistic regression, Tree model 등이 있습니다.
- 사례 기반 학습(Instance-Based Learning) : 모델을 미리 만들지 않고 새로운 데이터가 들어오면 바로 계산 시작 합니다. 예를 들어 K-NN, Naïve Bayes 알고리즘 등이 있습니다.
k값 정의 및 로직
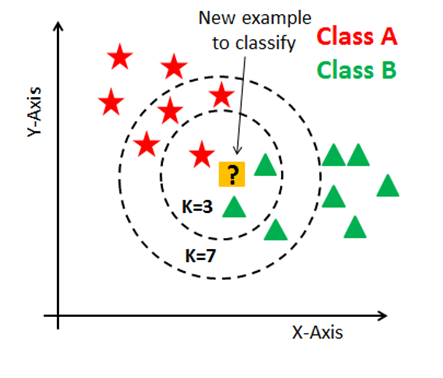
K-NN에서 k가 의미하는 것은 탐색할 이웃 수 입니다. 아래 그림을 통해 살펴보면 k=3일 때는 새로운 샘플이 Class B로 분류됩니다. 빨간색 1개, 녹색 2개 이므로 녹색에 속하게 됩니다.
이번엔 k=7일 때를 보겠습니다. 새로운 샘플이 Class A로 분류됩니다. 빨간색 4개, 녹색 3개 이므로 빨간색에 속하게 됩니다. 만약 k를 짝수로 하면 동점이 발생하게 되어 분류가 되지 않는 경우가 생깁니다. 그래서 동점이 되지 않도록 k값은 홀수 지정 합니다.
적절한 k값을 지정하기 위해서는 k를 조정해 가면서 가장 좋은 k값을 확인하는 작업을 합니다. grid search, random search 등의 방법을 활용할 수 있습니다.
K-NN 동작 원리(로직)
이번엔 동작 원리를 살펴 보겠습니다. K-NN은 1번~5번까지를 반복합니다.
- 먼저 새로운 데이터를 입력 받습니다.
- 모든 데이터들과의 거리를 계산합니다.
- 가장 가까운 K개의 데이터를 선택합니다.
- K개 데이터의 클래스를 확인합니다. (다수결 방식)
- 다수의 클래스를 새로운 데이터의 클래스로 예측
이렇게 fit 할때 훈련데이터가 저장되고, predict 하는 순간 거리를 계산하는 방식입니다.
K-NN에서 Overfitting vs Underfitting
k값을 늘릴수록 결정 경계는 더 부드러워지며 복잡도가 낮은 단순한 모델이 됩니다. k가 작은 경우는 모델의 복잡도가 높아집니다. 근처에 점 하나에 민감하게 반응하여 이상치(outlier)에 의해 오분류 가능성 생깁니다. 데이터의 지역적 특성을 지나치게 반영하여 Overfitting 발생할 가능성 있습니다.
반면, k가 클 경우 경계 완만해 지고 모델의 복잡도 낮아집니다. 다른 범주의 개체를 너무 많이 포함되어 잘못 분류할 가능성 있습니다. 이 것은 Underfitting이라고 할 수 있습니다.
마치며
K-NN의 특징과 알고리즘의 동작 원리에 대해 자세히 확인해 보았습니다. K-NN의 차원의 저주와 알고리즘의 장단점에 대해 궁금하시면 아래 글을 참고하시기 바랍니다.
K-NN(Nearest Neighbor) 차원의 저주, 장단점, weighted K-NN
K-NN(Nearest Neighbor) 차원의 저주, 장단점, weighted K-NN
이전 포스팅에서 K-NN 알고리즘의 특정에 대해서 살펴 보았다면 이번 포스팅에서는 장단점과 K-NN에서 왜 차원에 저주가 나타나는지에서 대해 포스팅해 보겠습니다. K-NN에서 전처리(pre-processing)
bommbom.tistory.com
'데이터 분석' 카테고리의 다른 글
| 의사결정나무(Decision Tree) 특징 및 동작 원리 - 불순도 알고리즘 (1) | 2023.09.18 |
|---|---|
| K-NN(Nearest Neighbor) 차원의 저주, 장단점, weighted K-NN (0) | 2023.09.17 |
| [머신러닝] 로지스틱 회귀 학습 - Log Loss, 크로스 엔트로피 (2) | 2023.09.14 |
| [머신러닝] 로지스틱 회귀 - 승산(Odds)과 활성화 함수 (0) | 2023.09.13 |
| [머신러닝] 로지스틱 회귀(Logistic Regression) - 선형 vs 비선형 (0) | 2023.09.12 |



