이번 포스팅에서는 로지스틱 회귀의 학습에 대해 설명을 드리도록 하겠습니다. 로지스틱 회귀에서 손실함수는 어떤 것을 사용할까요? 참고로 선형 회귀에 사용했던 손실함수인 최소제곱법(MSE)은 사용하지 않습니다. MSE를 사용할 경우 비선형 부분 때문에 중간에 학습을 멈추게 될 수도 있습니다. 로지스틱 회귀에서는 Log Loss(log likelihood)을 사용하여 파라미터를 최적화합니다. 보통 손실함수를 크로스엔트로피를 사용한다고 하는데, 크로스엔트로피(Cross entropy)는 negative log likelihood 입니다.
Log Loss 개념
Log Loss의 개념은 모델이 예측한 확률 값을 직접적으로 반영하여 평가하는 원리 입니다. 확률 값을 음의 log 함수에 넣어 변환시킨 값으로 평가를 하게 됩니다. 이 방식으로 잘못 예측할 수록, 페널티를 부여하는 방법입니다. 로지스틱 회귀는 이진 분류(1 또는 0)를 하기 때문에 로그 손실을 두개로 나눠서 처리하게 됩니다.
- y = 1 : 학생이 시험에 합격한 경우의 손실

- y = 0 : 학생이 시험에 탈락한 경우의 손실
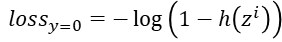
이 두 식을 하나의 식으로 표현하면 𝑐𝑜𝑠𝑡(ℎ(𝑥),𝑦)=−[𝑦 𝑙𝑜𝑔ℎ(𝑥)+(1−𝑦) log(1−ℎ(𝑥))] 과 같이 됩니다.
Log Loss 손실 적용 방식
Log Loss는 정확한 예측은 손실이 거의 없고, 잘못된 예측은 무한대에 가까운 큰 손실을 초래하는 특성이 있습니다.
- 이순신 합격했고 확률이 0.99이므로 잘 예측했으니 페널티 작고(↓)
- 홍길동 합격했으나 확률이 0.2로 잘못 예측했으므로 페널티 크게(↑)
| 이름 | 합격여부(y) | 합격 확률 | Log Loss |
| 이순신 | 1 | 0.99 | -log(0.99) = 0.01005 |
| 홍길동 | 1 | 0.20 | -log(0.2) = 1.6094 |
Probability vs Likelihood
우선 로지스틱 회귀 학습을 이해하기 위해 두개의 개념을 알아야 합니다. Probability와 Likelihood는 데이터 분포에 대한 이야기입니다. 손실함수 선택을 위해서는 데이터의 분포를 알아야 합니다. Probability(확률)은 특정 범위내에 얼마의 확률로 존재하는지를 말합니다. 이것은 면적(Area)으로 표현됩니다. 분포가 주어졌을데 데이터의 확률을 의미 합니다.
- 확률 = P(관측값 X | 확률분포 D)
Likelihood는 '우도' 또는 '가능도'라고 합니다. 분포에서 특정 사건이 일어날 가능성을 말합니다. 확률은 면적이라면 우도는 Point 값입니다. 좀 더 쉽게 풀어서 이야기 하면 데이터가 주어질 분포의 가능성(likehood)을 의미합니다.
- 가능도 = L(확률분포 D | 관측값 X)
이 우도의 개념을 활용한 최대우도법(MLE, Maximum likelihood method) 이 있습니다. 각 관측값에 대한 총 Likelihood 가 최대가되는 분포를 찾는 것을 말합니다. 결국, 이전 포스팅에서 계속 말해 왔던, 데이터를 가장 잘 설명해주는 분포를 찾는 방법과 일치합니다. 또 한가지는 딥러닝의 학습은 방금 설명한 MLE와 메커니즘이 같다라는 사실입니다. 결론적으로 로그-우도함수(Log likelihood function)가 최대 되는 점(𝛽)은 Cross-entropy가 최소가 되는 점가 같습니다.
Continuous variable vs Categorical variable
연속형 변수(Continuous variable)는 변수의 값 사이에 무수히 많은 다른 값들이 존재하는 경우를 말합니다. 연속형 변수가 타겟(Y) 값일 경우는 손실함수로 MSE 사용하는 것이 좋습니다. MSE의 특징은 초기값에 민감합니다.
반면 범주형 변수 (Categorical variable)는 이산형 변수라고도 불리우며 명목 변수, 순위 변수 값들인 경우 입니다. 범주형 변수는 손실함수로 Cross entropy를 사용합니다. Cross entropy는 초기값에 둔감한 편입니다.
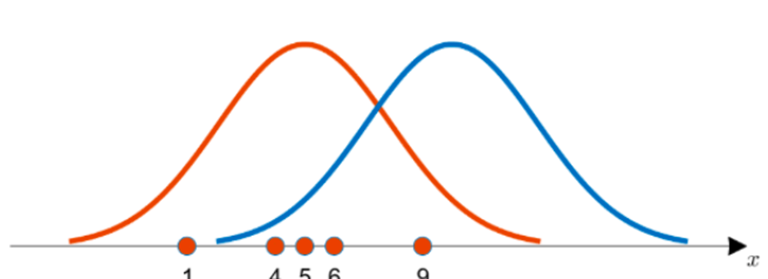
가우시안 분포 vs 베르누이 분포
가우시안 분포를 위키백과에서 찾아보면 확률론과 통계학에서 정규 분포 또는 가우스 분포는 연속확률분포의 하나라고 나옵니다. 통계학에서는 정규분포라 부르고 전기전자, 컴퓨터공학에서 가우시안 분포라고 합니다. 결국 가우시안 분포는 우리가 잘 알고 있는 정규분포를 이야기하는 것입니다. 앞에서 반복적으로 이야기 했던 처럼 Gaussian 분포의 최소화는 Mean Square Error와 최소화 하는 것과 같습니다.
베르누이 분포는 이산확률분포라고 불리기도 합니다. Bernoulli 분포를 최소화는 것은 Cross entropy를 최소화하는 것과 같습니다. 결론적으로 샘플 데이터의 분포와 Loss를 최소화하는 방향으로 학습을 수행합니다. 이것은 거의 비슷한 분포를 찾는 과정입니다.
Cross entropy란
엔트로피는 물리학에서 분자들의 무질서도 혹은 에너지 분산 정도를 나타내는 용어입니다. 여기서 착안하여 정보학에서 엔트로피는 정보의 양으로서 신호를 인식할 수 있습니다. 어떤 확률분포로 일어나는 사건을 표현하는 데 필요한 정보량을 의미합니다. 결국 교차 엔트로피(Cross entropy)는 두 가지 확률 분포가 얼마나 비슷한 지를 수리적으로 나타내는 개념 입니다. 만약 Cross entroy가 딥러닝에서 어떻게 사용되는지 알고 싶다면 확인하시 랍니다.
Cross entropy 학습
만약 q는 딥러닝 모델의 추정 확률분포라고 하고 p는 딥러닝 모델이 추구해야 할 미지의 확률분포를 의미한다고 가정하겠습니다.
- 이때 q와 p를 활용하여 교차 엔트로피를 계산합니다.
- 이 교차 엔트로피가 낮아지는 쪽으로 모델의 추정 확률분포 q를 꾸준히 개선시킵니다.
- 확률분포 q를 확률분포 p에 가깝게 접근시키는 것이 학습 원리입니다.
실제 값과 예측 값이 맞는 경우에는 0으로 수렴하고 값이 틀릴 경우에는 값이 커지기 때문에 두 확률분포가 서로 얼마나 다른 지를 나타내 주는 정량적인 지표입니다.
'데이터 분석' 카테고리의 다른 글
| K-NN(Nearest Neighbor) 차원의 저주, 장단점, weighted K-NN (0) | 2023.09.17 |
|---|---|
| K-NN(Nearest Neighbor) 알고리즘 - 사례 기반 학습 (0) | 2023.09.15 |
| [머신러닝] 로지스틱 회귀 - 승산(Odds)과 활성화 함수 (0) | 2023.09.13 |
| [머신러닝] 로지스틱 회귀(Logistic Regression) - 선형 vs 비선형 (0) | 2023.09.12 |
| [머신러닝] 선형 회귀 가정과 다중공선성 진단 및 해결 방법 (2) | 2023.09.11 |



