이전 포스팅에서는 로지스틱 회귀의 특징에 대해 살펴 보았습니다. 이번 포스팅에서는 로지스틱 회귀의 계산 방식을 유도해 보게습니다. 알아야 될 개념인 승산(Odds)에 대해 알아보면서 로지스틱 함수까지 유도되는 것을 확인 할 수 이습니다.
로지스틱 회귀 알고리즘이 딥러닝(deep learning)에서는 활성화 함수로 주로 활용됩니다. 그 부분에 대해서도 자세히 살펴 보겠습니다.
Odds(아드, 오즈) 란
Odds는 사람에 따라 아드, 오즈로 부릅니다. 승산은 성공확률 P를 정의할때, 실패(0)에 대한 성공(1)의 비율을 의미합니다. 그래서 범위는 0 < odds < ∞ 입니다. 수식은 간단하게 $ Odds = \frac{𝑃}{(1−𝑃)} $ 로 정의할 수 있습니다.
- 𝑝=1 → O𝑑𝑑𝑠 = ∞
- 𝑝=0 → O𝑑𝑑𝑠 = 0
좀 쉽게 이해하기 위해서 예를 들어 보겠습니다. 우리나라 축구 경기 우승을 예측한다고 하겠습니다. 2(우승) : 11(우승 못함) 으로 예측했을 때 승산과 우승 확률은 다음과 같습니다.
- 승산(Odds) = 2/11
- 우승확률 = 2/13 = 약 15%
보는 것과 같이 승산(Odds)은 우리가 생각하는 (우승) 확률과 다릅니다. '우승 못함' 예측에 대한 '우승' 예측의 비율이라고 보면 됩니다. 우리가 익숙한 우승 확률은 '우승 못함 + 우승' 즉 전체에서 '우승'에 비율 입니다. 그 차이점을 인지하시면 로지스틱 회귀를 이해하는데 도움이 됩니다.
Odds에서 로지스틱 함수까지 유도
로지스틱 모형의 식은 독립 변수가 (-∞,∞)의 어느 숫자이든 상관 없이 종속 변수 또는 결과 값이 항상 범위 [0, 1] 사이게 있게 하는 것입니다. Odds는 참/거짓 비율에서 참이 거짓보다 얼마나 높은가에 대한 것이라고 앞에서 알아 보았습니다. 다음으로 알아야할 것이 Logit 변환 입니다. Logit 변환은 Odds에 자연로그를 취한 함수를 말합니다.
- 수식 = ln 𝑃/(1−𝑃)
- 좌변(x)의 범위는 0 ~ 1 값을 입니다.
- 우변(y)의 범위는 –∞에서 + ∞ 까지 값을 가집니다.
다음으로 Logistic 함수는 Logit변환을 직선의 식(ax=b)과 같다는 방정식을 P에 대해 풀면 나오는 함수 입니다. 수식은 아래와 같습니다.

Logistic 함수의 예측값이 0~1 사이로 고정되는 것이 아니라, 0보다 작을 수도 있고, 1보다 클 수 도 있습니다. 따라서 결과값이 이분항으로 나올때는 로지스틱 함수를 사용 합니다.
Odds Ratio(승산비)
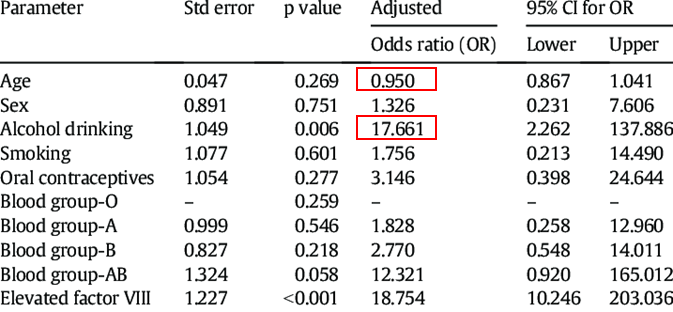
Odds를 데이터를 분석할 때도 활용할 수 있습니다. Odds Ratio(승산비)는 나머지 입력변수 모두 고정, 한 변수를 1단위로 증가시켰을때 변화하는 Odds의 비율을 말합니다. 논문 등에서도 Odds ratio를 보여주는 경우가 있습니다. 그 데이터를 이용하여 우리는 아래와 같이 해석할 수 있습니다.
- 나이가 1년 더 많으면 병의 걸릴 확율 0.95 증가 합니다.
- 알코올 1병 더 마실때 마다 병의 걸릴 확율 17.661 증가 합니다.
활성화 함수(Activation Function)
로지스틱 함수가 왜 활성화 함수에 사용 될까요? 활성화 함수는 이전 층(layer)의 결과값을 변환하여 다른 층의 뉴런으로 신호를 전달하는 역할을 합니다. 신호 전달의 0, 1을 로지스틱 함수로 할 수 있기 때문입니다. 활성화 함수를 비선형 함수를 사용하는 이유는 선형은 아무리 깊어지더라도 f(ax+by)=af(x) + bf(y)의 성질 때문에 결국 하나의 layer로 구현할 수 있게 됩니다. 결론적으로 linear한 연산을 갖는 layer를 수십개 쌓아도 최종적으로는 하나의 linear 연산으로 표현되어 버리는 것입니다. 그래서 깊은 Layer를 쌓아서 특성을 추출하기 위해서는 비선형 함수가 적합니다.
Sigmoid 함수
Sigmoid 또는 Logistic 함수는 확률을 출력으로 예측해야 하는 모델에 일반적으로 사용합니다. 확률은 0과 1 사이에만 존재하게 됩니다. 대부분 활성화 함수로 사용하지 않지만 유일하게 binary classification의 출력층 노드에서 0~1사이 값을 만들고 싶을때 사용합니다. Sigmoid의 장점은 출력값의 범위가 (0, 1)로 제한하기에 정규화 관점에서 exploding gradient 문제를 방지 합니다. 단점은 Vanishing gradient 문제를 발생하고 시그모이드 함수의 출력은 0을 중심으로 대칭이 아니기에 모든 뉴런의 출력은 동일한 부호(모두 양수 또는 모두 음수의 형태)가 되므로 비용 및 효율면에서 좋지 못합니다.
하이퍼블릭 탄젠트(Hyperbolic Tangent) 함수
시그모이드 함수값의 중심을 0으로 맞추기 위해 개선된 함수 입니다. 결과값이 (-1, 1) 사이이면서 양수와 음수가 나오는 비중이 비슷하기 때문에 zigzag 현상이 덜합니다.
렐루(ReLU : Rectified Linear Unit) 함수
ReLU는 입력값이 양수인 경우만 뉴런을 전달하는 함수 입니다. 시그모이드나 tanh보다 손실함수의 수렴속도가 6배 정도 빠릅니다. 하지만 함수값의 중심이 0이 아니기 때문에 Dying ReLU 문제가 발생합니다.
그렇다면 어떤 활성화 함수를 사용하는게 좋을까요? 일반적으로 ReLU 함수를 많이 사용합니다. ReLU를 적용해 보고 다른 활성화 함수를 시도해보면서 더 좋은 학습 효율을 찾는 방법 사용하는 것이 좋습니다.
'데이터 분석' 카테고리의 다른 글
| K-NN(Nearest Neighbor) 알고리즘 - 사례 기반 학습 (0) | 2023.09.15 |
|---|---|
| [머신러닝] 로지스틱 회귀 학습 - Log Loss, 크로스 엔트로피 (2) | 2023.09.14 |
| [머신러닝] 로지스틱 회귀(Logistic Regression) - 선형 vs 비선형 (0) | 2023.09.12 |
| [머신러닝] 선형 회귀 가정과 다중공선성 진단 및 해결 방법 (2) | 2023.09.11 |
| [머신러닝] 선형 회귀 - 옵티마이저와 학습률(Learning Rate) (0) | 2023.09.10 |



