이번에는 차원 축소 기법 중 t-SNE에 대해 알아보도록 하겠습니다. t-분포 확률적 임베딩이라고 우리말로 번역할 수 있는데요. 이 알고리즘을 보통은 '티스니'라고 읽습니다. 하지만 '티-에스엔이'라고 그대로 읽는 사람도 있습니다. 읽는 방법은 분석가 마다 편하게 부르기 때문에 너무 규정하지 않는게 좋습니다.
이 알고리즘은 2002년 샘 로이스(Sam Rowise)와 제프리 힌튼에 의해 개발되었는데요. t-SNE는 고차원 데이터에 적합하다고 알려져 있습니다. 특히 2, 3차원으로 줄여 가시화하는데 유용하죠.
t-SNE (t-distributed Stochastic Neighbor Embedding)
t-SNE는 t-분포를 활용해 고차원의 공간에 존재하는 data x의 neighbor 간의 distance를 최대한 보존하도록 만듭니다. 그 보존된 data에 대응되는 저차원의 y를 학습하는 방법론입니다. 분포의 분산뿐만 아니라 이웃까지 거리까지도 고려한 알고리즘이라고 할 수 있습니다. 차원 축소 중 고차원 data를 시각화하는 최근 가장 인기 많은 알고리즘입니다. 비정형 데이터 분석에 사용하며, non-linear 방법에 속합니다.
t-SNE와 PCA의 차이점은 무엇일까요?
데이터 점들을 1차원으로 투영 시켰을 때 PCA는 거리가 가깝거나 멀거나 변별력이 없는 문제가 있었습니다. 다른 표현으로 PCA로는 멀리 있는 점도 결국 모두 같게 표현되어 버린다는 단점이 있었습니다.
t-SNE의 아이디어는 데이터 포인트 사이의 거리를 가장 잘 보존하는 표현을 찾아보자는 것이었습니다. 그렇게 하기 위해 멀리 떨어진 포인트보다 가까이 있는 포인트에 더 많은 비중은 주는 방식을 택할 수 있습니다. PCA(주성분 분석)의 단점을 보완한 알고리즘이라 말할 수 있습니다.
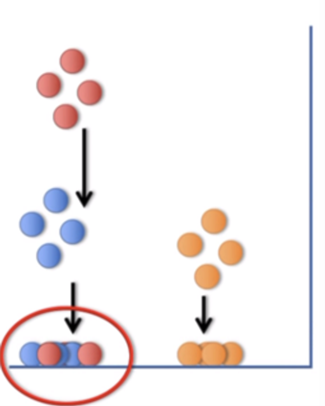
t-SNE 동작 원리
1. neighboring graph 를 base로 합니다.
2. Local neighbor structure를 보존합니다. (고차원의 벡터의 유사성이 저차원에서도 유사하도록 보존)
- 고차원의 Probabilties p를 계산
- 저차원의 Probabilties q를 계산
- 두 분포 차이를 반영한 cos function C(p, q) 정의
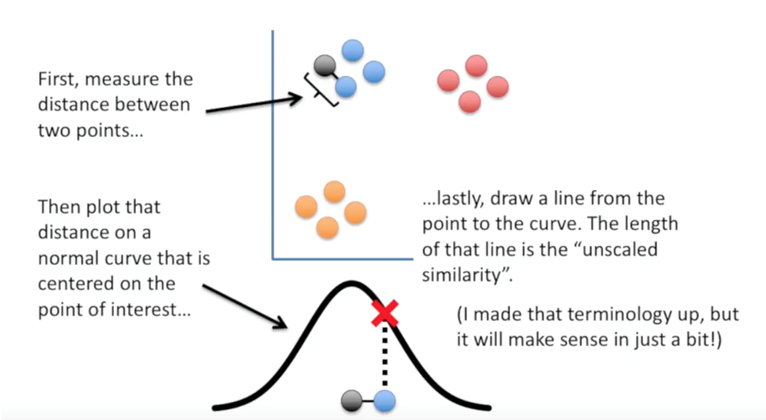
3. t-분포를 이용해 하나의 기준점을 정하고 모든 다른 데이터와 거리를 구합니다.
4. 그 값에 해당하는 t-분포 값을 선택 후 값이 유사한 데이터끼리 묶어줍니다.
5. 비용함수(Cost Funcation)이 최소화 되도록 저차원 데이터로 변환합니다.
단점 및 문제점
- 성능측면에서 데이터의 개수가 n개라면 연산량은 n의 제곱만큼 늘어납니다.
- 매번 돌릴 때마다 다른 시각화 결과가 나옵니다. 초기 기준점에 따라 달라진다는 의미입니다.
- 오로지 2, 3차원으로만 줄일 수 있습니다. 4차원 이상은 지원하지 않습니다.
- 초고차원의 데이터를 10차원 정도로 줄이는 것은 불가능하므로 모델을 구현하기에는 적합한 차원축소가 아닙니다.
'데이터 분석' 카테고리의 다른 글
| 모수 vs 비모수 모델 - 파라미터 vs 하이퍼파라미터 (1) | 2023.10.12 |
|---|---|
| 차원 축소 - 특잇값 분해(SVD) 및 PCA 관계 (0) | 2023.10.11 |
| 차원 축소 - PCA(주성분 분석), Explained Variance Ratio (1) | 2023.10.10 |
| 차원축소 - 투영과 매니폴드(manifold) 학습은 어떻게 다른가? (0) | 2023.10.10 |
| [머신러닝] Feature Selection 방법 - Filter, Wrapper, Embedded (0) | 2023.10.06 |



