이번 포스팅에서는 딥러닝에서 미분이 왜 필요하고 딥러닝에서 중요한 미분 공식 5가지에 대해서도 살펴보도록 하겠습니다. 딥러닝을 배우다 보면 손실함수의 대한 미분, 수치미분, 편미분이라는 용어들이 나오게 되죠. 왜 딥러닝은 미분과 밀접한 관계가 있는지 알아보도록 하겠습니다.
손실함수에 미분은 왜 필요한가?
손실함수(Loss Funcation)는최적의 매개변수를 찾는 과정이라고 했습니다. 최적의 매개변수를 찾기 위해 미분을 사용한다는 이야기인데요. 미분은 입력변수 x가 미세하게 변할 때 함수 f(x)가 얼마나 변하는지 알 수 있는 식입니다. 손실함수 f(x)는 입력 x의 미세한 변화에 얼마나 민감하게 반응하는지 그 기울기를 계산하기 위해 미분이라는 방법을 사용합니다.
- 미분계수 : 순간변화율 = 접선의 기울기
- 특정 구간의 평균변화율을 계산하는 것처럼 구간을 거의 0으로 하는 순간의 변화율을 계산
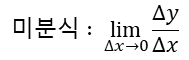
이런 미분을 실제 생황에서 우리는 어디에 사용할까요? 물체속도, 온도변화, 3D프린터, 애니메이션, CG기술, 학습곡선, 스포츠 순각속도, 도로설계 등 많은 분야에 사용하고 있습니다. 우리가 수학시간에 배웠던 미분이 이렇게 활용 하는데가 많습니다.
수치미분
그렇다면 수치미분은 무엇일까요? 임의 두 점에서의 함수 값들의 차이를 차분이라고 하며, 이렇게 아주 작은 차분으로 미분하는 것을 수치 미분이라 합니다. 처음에 딥러닝의 기울기를 구할 때는 수치미분을 사용하여 계산하는 방법을 사용했습니다. 그런데 여러 가지 문제들이 있었습니다.
1. 반올림 오차 문제
- ∆x → 0에 작은 값 10e-50을 대입하면 반올림 오차(rounding error) 문제가 발생
- 이는 작은 값(예를 들어 소수점 8자리 이하)이 생략되어 최종 계산 결과에 오차가 생기는 문제
- 가장 작은 값을 대입하기 위해 $ 10^{−4} $ 값을 넣은 것이 적합
2. 함수 f의 차분 문제
- 진정한 접선과 근사로 구한 접선의 오차를 극복하기 위해 (x+h)와 (x-h) 사이의 함수 f의 차분을 계산함, 엄밀히 일치하지 않음
- 예를 들어, "f(x+h) – f(x−h)" /(2∗ℎ)
3. 수치미분의 한계
- 계산량이 많아 속도가 오래 걸림
- ((입력 피처수)x(1층 노드수)+(1층 노드수 x출력 수)) x 학습 회수
수치미분의 문제들을 보안해도 결국 수치미분의 한계는 있었습니다. 계산량이 너무 많아서 속도가 오래 걸린다는 것이었죠. 이렇게 되면 거의 활용하기 어려운 모델이 됩니다. 그래서 대안으로 각 층에서의 미분을 공식화하여 미분 과정을 단순화하는 방법을 사용하게 됩니다. 그게 바로 우리가 잘 알고 있는 ‘오차역전파(Backpropagation)'로 계산하는 방식입니다.
딥러닝에서 중요한 미분 5가지 공식
오차연전파(Backpropagation)를 이용해서 계산하는 방식은 아래와 같은 미분 공식을 사용하게 됩니다. 그런데 가장 많이 사용하는 미분 공식 5가지를 소개합니다. 이 공식들을 수식으로 풀는 과정은 생략하겠습니다. 중요한 것은 아래 5가지는 외우셔야 딥러닝의 계산과정을 따라갈 수 있습니다.
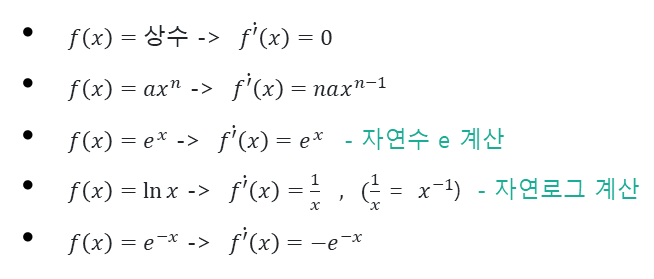
편미분은 왜 할까?
신경망의 계산을 오차역전파로 진행할 때 편미분을 사용하게 됩니다. 편미분은 입력변수가 하나 이상인 다변수 함수에서 사용하는 데요. 딥러닝은 변수가 많기 때문에 편미분을 사용해야 하는 게 맞겠죠. 편미분은 미분하고자 하는 변수 하나를 제외한 나머지 변수를 상수 취급하고, 해당 변수를 미분하는 방법입니다. 예를 들어, 𝑓(𝑥,𝑦)=를 변수 x에 대하여 편미분 할 경우 (𝜕𝑓(𝑥,𝑦))/𝜕𝑥 라고 합니다. 그러면 아래의 문제를 풀어보도록 하시죠.
문제 : 𝑓(𝑥, 𝑦)=2𝑥+3𝑥𝑦+𝑦^3
- 변수 x에 대한 편미분 = 2+3𝑦+0
- 변수 y에 대한 편미분 = 0+3𝑥+3𝑦^2
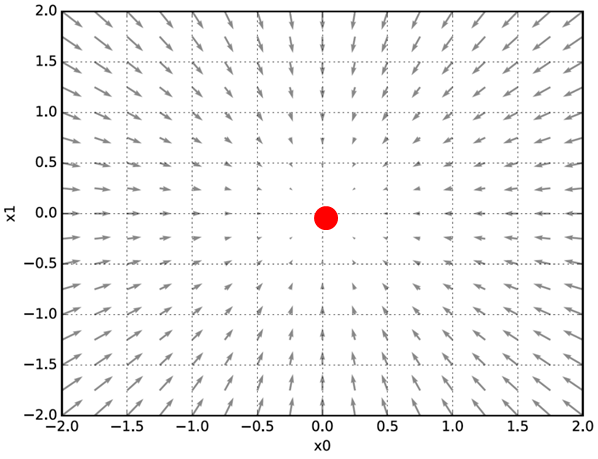
위의 그림과 같이 편미분을 통해 손실의 최저점(빨간원)을 찾아갑니다. 체중(야식, 운동) 함수가 있다고 가정하면 아래와 같은 편미분 식이 나오죠.
- 현재 먹는 야식의 양에서 조금 변화를 줄 경우 체중은 얼마나 변하는지 -> 𝜕체중/𝜕야식
- 현재 하고 있는 운동량에 조금 변화를 줄 경우 체중은 얼마나 변하는지 -> 𝜕체중/𝜕운동
기울기
(x0, x1) 양쪽의 편미분을 모두 묶어(𝜕𝑓/𝜕𝑥0 , 𝜕𝑓/𝜕𝑥1) 처럼 모든 변수의 편미분을 벡터로 정리한 것을 기울기(gradient)라고 합니다. 기울기는 그림에서 함수의 가장 낮은 최소값을 가리킵니다. 기울기가 가르키는 방향은 손실함수 출력값을 가장 크게 줄이는 방향을 나타내죠. 결국 기울기가 가장 낮은 지점에서 최저점을 형성합니다.
'딥러닝' 카테고리의 다른 글
| 딥러닝 모델 일반화(regularization) 총정리 (1) | 2024.01.24 |
|---|---|
| 딥러닝 하이퍼파라미터 튜닝 및 설정 (0) | 2024.01.23 |
| 딥러닝 학습 방법: batch size, Iteration, epoch(에포크) (0) | 2024.01.19 |
| 딥러닝에서 크로스 엔트로피(Cross Entropy)를 사용하는 이유 (0) | 2024.01.18 |
| 딥러닝에서 손실함수를 사용하는 이유 (0) | 2024.01.17 |



