이번 포스팅에서는 손실함수에 대해 다뤄보겠습니다. 머신러닝에서도 손실함수는 사용하게 되는데요. 그렇다면 딥러닝에서는 손실함수를 어떻게 사용할까요?
손실함수를 사용하는 이유?
신경망 학습은 최적의 매개변수 값을 찾는 과정입니다. 방법은 미분(기울기)을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복하죠. 결론적으로 높은 정확도를 끌어내는 매개변수 찾기 위해 사용 손실함수를 사용한다고 할 수 있습니다.
정확도를 높이기 위한다면 정확도 자체를 사용해도 되지 않을까 생각할 수도 있는데요. 정확도가 아닌 손실함수를 사용하는 이유는 정확도는 '0' 이되는 지점이 지점이 생기기 때문입니다. 하지만 손실함수는 활성화 함수가 기울기가 0이 되지 않는 함수라 절대 '0'이 되지 않게 되어있습니다. 그렇다면 손실(Loss)을 구하기 위한 Back propagation의 가정에 대해 알아보겠습니다.
Back propagation 적용을 위한 가정
- Training data 전체의 Loss function은 각각의 loss에 대한 합(sum)임
- 신경망(Network) 출력 값과 타켓값에 대해서 Loss를 구함
- 경사하강법에 의해 출력층부터 계산된 Gradient값에 Local Gradient를 곱하는 식으로 수행
- Gradient가 뒤에서부터 전달하여 전체를 Layer를 계산함
- 이러한 가정에 부합하는 손실함수로 MSE, Crossentropy를 사용함
손실함수의 종류
- 회귀 모델 사용 손실함수 : MSE, MAE, RMSE 등
- 분류 모델 사용 손실함수 : Binary cross-entropy, Categorical cross-entropy 등
- 딥러닝 학습 : 평균제곱오차(MSE)와 교차 엔트로피 오차(cross entropy error)를 사용
- 어떤 손실함수를 사용할지는 데이터의 분포 등의 특성에 따라 선택
- 아래의 연속형 변수 vs 범주형 변수, 가우시안 분포 vs 베르누이 분포에 따라 다름
Continuous variable vs Categorical variable
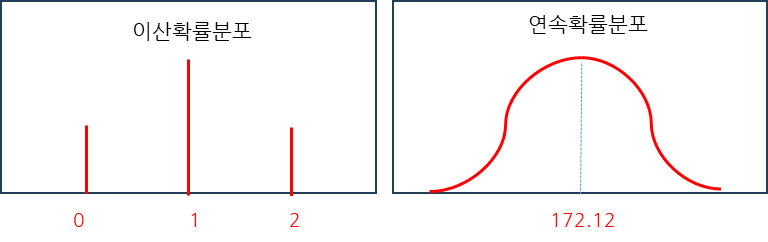
Continuous variable(연속형 변수)
- 변수의 값 사이에 무수히 많은 다른 값들이 존재하는 경우
- 손실함수로 MSE 사용
- MSE는 초기값에 민감함
Categorical variable(범주형 변수)
- 이산형 변수라고도 하며 명목 변수, 순위 변숫값들인 경우
- 손실함수로 Cross entropy 사용
- Cross entropy는 초기값에 둔감함
가우시안 분포 vs 베르누이 분포
가우시안 분포
- 확률론과 통계학에서 정규 분포 또는 가우스 분포는 연속확률분포의 하나이다.(위키백과)
- 통계학에서는 정규분포라 부르고 전기전자, 컴공에서 가우시안 분포라고 함
- Gaussian 분포의 최소화는 Mean Square Error와 같음
베르누이 분포
- 이산확률분포
- Bernuoulli 분포의 최소화는 Cross entropy와 같음
샘플 데이터의 분포와 Loss를 최소화하는 방향으로 학습을 수행함, 거의 비슷한 분포를 찾는 과정
'딥러닝' 카테고리의 다른 글
| 딥러닝 학습 방법: batch size, Iteration, epoch(에포크) (0) | 2024.01.19 |
|---|---|
| 딥러닝에서 크로스 엔트로피(Cross Entropy)를 사용하는 이유 (0) | 2024.01.18 |
| 소프트맥스 함수를 사용하는 이유? (0) | 2024.01.16 |
| 활성화 함수 종류: 왜 활성화 함수가 필요할까? (1) | 2024.01.15 |
| 신경망 연산: 딥러닝 가중치 계산 방법 (0) | 2024.01.12 |



