오차역전파가 딥러닝에 발전에 많은 영향을 미쳤다는 것을 "퍼셉트론과 오차역전파" 라는 글에서 이야기한 적이 있습니다. 이번 글은 오차역전파의 원리와 계산하는 방법을 자세히 알아 보겠습니다.
오차역적파와 계산 그래프
오차역전파를 이해할려면 계산 그래프를 알아야 합니다. 오차역전파는 가중치 매개변수의 기울기를 효율적으로 계산하는 방법인데요. 오차역전파를 이해하는 방법은 계산 그래프를 이용한 수식 계산입니다. 그래서 개산 그래프는 말 그래도 계산 과정을 그래프로 나타내는 방법입니다. '밑바닥부터 시작하는 딥러닝' 이라는 책에서 계산 그래프를 통해 설명하고 있죠.
계산 그래프는 노드(node)와 에지(edge, 노드사이 직선)로 표현할 수 있습니다. 계산 그래프 구성하는 방법은 데이터와 연산자를 모두 노드로 연결(에지)하는 방식입니다.
텐서플로우 계산 그래프
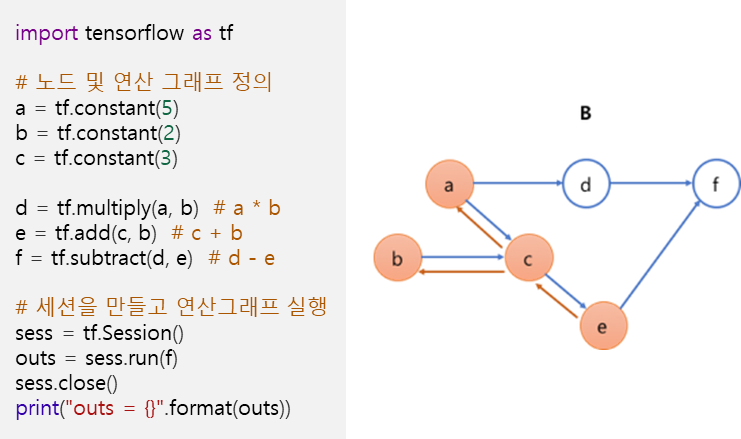
그런데 텐서플로우도 계산 그래프라는 개념이 있습니다. 계산 그래프는 계산의 흐름을 방향성 그래프로 표현하는 개념입니다. 그래프는 노드가 작업을 나타내고 가장자리가 이러한 작업 간의 데이터 흐름(텐서)을 나타내는 구조로 정의합니다. 이는 TensorFlow 1.0 방식으로 2.0도 지원하지만 계산 그래프를 설계하기 보다는 개발이 쉬운 접근 방식으로 변경됐습니다.
- Data Flow Graph : 텐서플로우에서 사용하고 있으며 노드를 연결하는 엣지가 있고, 이 엣지가 수행하는 연산 역할을 하는 그래프 구조를 의미
- Data Flow Graph Computation : 데이터가 edge역할을 하여 node로 흘러가는 그래프 구조를 갖으며 node에 지정된 연산을 하는 연산방법
왜 계산 그래프로 계산할까?
그러면 왜 계산 그래프로 계산할까요? 그 이유는 아래 세가지 때문입니다.
1.국소적 계산
- 아무리 복잡한 계산이라도 각 노드의 단순한 계산에만 집중하여 문제를 단순화
- 작은 계산으로 분할하여 조립 라인 작업으로 결과를 다음 노드에 전달
2.미분의 계산
- 역전파을 이용한 Chain rule 방식으로 미분의 효율적 계산 수행
3.연산량 최소화
- 노드 e는 노드 c에 직접 의존, 노드 a, b는 간접 의존 관계
- 노드 e를 계산하기 위해서 노드 c,b,a만 계산해 주면 되며, 그래프를 통해 노드의 모든 의존 관계 파악
- 이런 방식은 연산량을 최소화하면서 모든 의존 관계를 파악할 수 있음
연쇄법칙(Chain rule)
함성함수는 두 개의 함수를 이용해서 새로운 하나의 함수를 얻을 수 있는 함수를 말합니다. 예를 들어, \( 𝑧=(𝑥+𝑦)^2 \) 은 \( 𝑧=𝑡^2, 𝑡=𝑥+𝑦 \) 두개 식으로 구성됩니다. 합성함수를 미분하기 위해 ‘합성함수를 구성하는 각 함수의 미분곱’ 으로 나타내는 것을 연쇄법칙(chain rule)이라고 합니다. 연쇄법칙에 의해 구해진 (편)미분값이 결국 그 노드의 영향도(얼마나 영향을 주는지에 대한 수치)에 해당합니다.
\( 𝑓(𝑥)=𝑒^{−𝑥} \) 를 Chain rule로 미분해 보겠습니다.
- $ 𝑡=−𝑥 $ 놓으면 $ 𝑓(𝑥)=𝑒^𝑡 $
- $ \dfrac{𝜕𝑓}{𝜕𝑥} = \dfrac{𝜕𝑓}{𝜕𝑡} \dfrac{𝜕𝑡}{𝜕𝑥} $ → Chain rule 적용(약분 개념)
- $ =\dfrac{𝜕(𝑒^𝑡)}{𝜕𝑡} \dfrac{𝜕(−𝑥)}{𝜕𝑥}=(𝑒^𝑡 )(−1) $ → $ 𝑒^𝑡 $ 미분하면 $ 𝑒^𝑡 $
- $ =(𝑒^{−𝑥})(−1)= -𝒆^{−𝒙} $ → 𝑡=−𝑥 대입(t는 다시 x의 형태로 만듦)
뎃셈(bais), 곱셈(weight) 계층 구현
덧셈 역전파는 상류값을 그대로 흘려보내서 순방향 입력신호 불필요합니다. 미분값이 1이기 때문에, 출력에서 온 값이 그대로 전달됩니다.
곱셈 역전파는 순전파 때 입력신호를 ‘서로 바꾼 값‘을 곱하기 때문에 달라집니다. 순방향 입력 신호값이 필요해 변수 저장이 필요합니다.
Feedforward Propagation
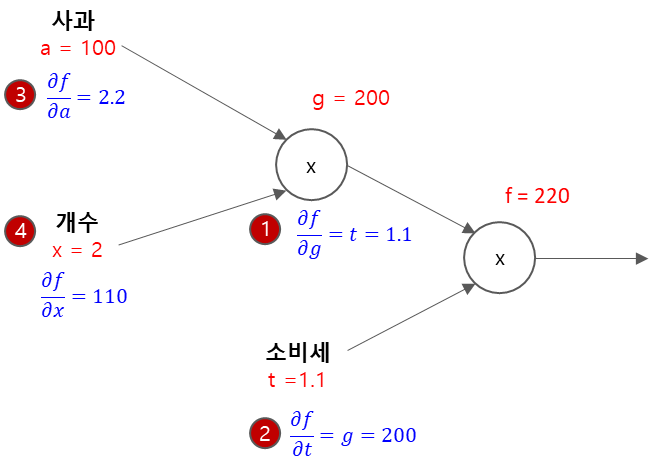
$ a=100, x=2, t=1.1 $
Back Propagation
수식 : $ f = a * x * t $
$ g = a∗𝑥 → \dfrac{𝜕𝑔}{𝜕𝑎} = 𝑥, \dfrac{𝜕𝑔}{𝜕𝑥} = 𝑎 $
$ f = g∗𝑡 → \dfrac{𝜕𝑓}{𝜕𝑔} = 𝑡, \dfrac{𝜕𝑓}{𝜕𝑡} = 𝑔 $
- $ \dfrac{𝜕f}{𝜕g}= t = 1.1 $
- $ \dfrac{𝜕f}{𝜕t} = g =200 $
- $ \dfrac{𝜕f}{𝜕a}= \dfrac{𝜕f}{𝜕g} \dfrac{𝜕g}{𝜕a} = t∗x = 1.1∗2 = 2.2 $
- $ \dfrac{𝜕f}{𝜕x}= \dfrac{𝜕f}{𝜕g} \dfrac{𝜕g}{𝜕x} = t∗a = 1.1∗100 = 110 $
'딥러닝' 카테고리의 다른 글
| 신경망 매개변수 갱신: 옵티마이저 (0) | 2024.01.29 |
|---|---|
| 오차역전파 알고리즘: ReLU, Sigmoid, Affine, Softmax 계산 (0) | 2024.01.26 |
| 딥러닝 모델 일반화(regularization) 총정리 (1) | 2024.01.24 |
| 딥러닝 하이퍼파라미터 튜닝 및 설정 (0) | 2024.01.23 |
| 딥러닝의 수치미분과 편미분: 꼭 알아야 할 미분 공식 (1) | 2024.01.22 |



