아마 정규 분포를 모르시는 분은 없을 것입니다. 정규 분포는 '가우시안 분포'라고도 합니다. 통계학을 모를 때는 가우시안 분포는 어떤 분포지? 정규 분포하고 다른 것인가 하고 찾아보기도 하죠. 그런데 같은 것입니다. 이 글에서는 왜 통계학에서 정규 분포를 중요하게 생각하는지 알아보도록 하겠습니다.
중심 극한 정리
정규 분포를 유래를 알려면 중심 극한 정리를 이야기 해야 합니다. 우리가 세상에서 발생하는 무작위로 여러 가지 일이 있습니다. 만약, 주사위를 굴려 얻은 숫자를 기록한다고 가정해 보겠습니다. 이제 계속해서 주사위를 여러 번 굴리고 매번 발생한 건수를 계산하다 보면 흥미로운 점을 발견하게 됩니다.
기본적으로 주사위 숫자의 모양이 어떤 종류인지에 관계없이(예: 실제로 퍼져 있거나 뭉쳐져 있는 경우) 여러 숫자를 더하면 전체가 점점 더 비슷해 보이는 경향성을 띄게 됩니다. 이 모양이 정규 분포라고 불리는 형태입니다.
이러한 정규 분포는 실제로 예측 가능하고 작업하기 쉽기 때문에 매우 편리합니다. 따라서 원래 숫자가 어떤 패턴을 따르지 않더라도 일단 합산하면 총합이 종 모양의 곡선처럼 보이기 시작합니다. 이것이 바로 중심극한정리입니다.
우리는 여기서 알 수 있습니다. 충분히 큰 표본 크기가 주어지면 원래 분포에 관계없이 모든 모집단에서 정규 분포로 나타난다는 사실입니다. 이 정리는 표본 데이터에서 모집단 매개변수에 대한 추론을 가능하게 하므로 통계의 기본입니다.
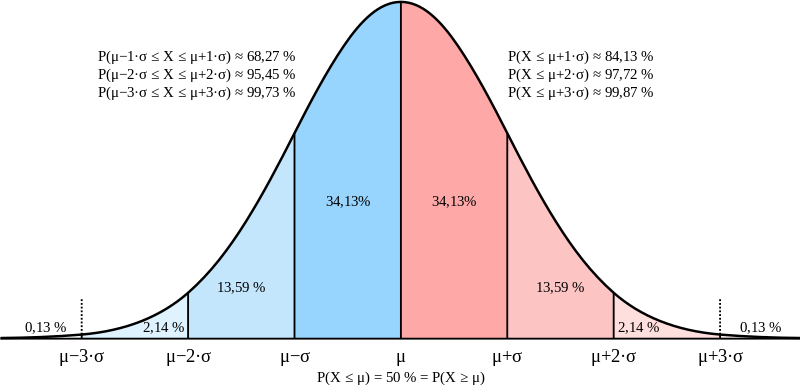
정규 분포를 어떻게 사용할까?
실제 세계의 많은 자연 과정과 측정값은 정규 분포에 가깝습니다. 예를 들어 키, 몸무게, IQ 점수, 측정 오류 등이 이에 해당합니다. 따라서 정규 분포는 이러한 현상을 모델링하고 통계 분석을 단순화하는 데 유용한 근사치 역할을 합니다. 모델링을 하려면 우리가 정답이라고 하는 분포에 가깝게 알고리즘을 만들어야 하는데, 정규 분포가 그 기준이 되어 주는 것입니다.
1. 통계적 추론
정규 분포에는 통계적 추론(예: 가설 테스트 및 신뢰 구간)을 다루기 쉽습니다. 다루기 쉽다는 말은 계산이 가능한 정의된 속성이 있다는 이야기 입니다. 이를 통해 계산이 단순화되고 데이터에서 예측하고 결론을 도출할 수 있습니다.
2. 모수적 테스트
t-Test, ANOVA(분산 분석), 선형 회귀 등 많은 통계 테스트에서는 데이터가 정규 분포를 따른다고 가정합니다. 이러한 테스트는 이 가정이 위반되서는 안됩니다. 하지만 이 정규성 가정은 일반적으로 데이터의 해석을 단순화하고 결과의 타당성을 향상시킵니다.
3. 표준화
정규 분포는 평균과 표준 편차를 특징으로 하며 이를 통해 데이터를 표준화하는 것이 가능합니다. 표준화는 데이터를 z-score로 변환하여 다양한 데이터 세트를 비교합니다. 분포 내 개별 데이터 포인트의 상대적 위치를 해석하는 것이 사실 더 쉽다고 할 수 있죠. 정규화와 표준화의 차이점은 링크를 참고하시기 바랍니다.
정규 분포의 한계
전반적으로 정규분포는 이론적 특성, 폭넓은 적용 가능성, 데이터 분석 및 추론에 대한 실질적인 의미로 인해 통계에서 중요한 역할을 합니다. 하지만 모든 데이터(현상)이 정규 분포를 보이는 것은 아니니 무작정 가정하는 것은 주의해야 합니다. 따라서 데이터 세트가 정규 분포를 보이는지 아닌지를 판단하는 것이 우선되어야 합니다.
'데이터 분석' 카테고리의 다른 글
| Data Imputation(데이터 대치, 결측치 처리) 및 흔한 실수들 (0) | 2024.04.30 |
|---|---|
| 가설 검정 왜 필요할까? t-test, ANOVA, 카이제곱 검정 (0) | 2024.04.29 |
| 피처 엔지니어링(Feature engineering) 방법, 단계별 종류 및 특징 (1) | 2024.04.05 |
| 머신러닝, 딥러닝 데이터 양이 충분한지 확인하는 방법 (0) | 2024.04.04 |
| 상관관계를 이용하는 이유 (0) | 2024.04.02 |



