이번 포스팅에서는 딥러닝에서 표기법과 하이퍼 파라미터에 대해 알아보겠습니다. 신경망은 많은 부분 그림을 통해 설명을 하기 때문에 가중치의 표기법이 필요한 이유입니다.
가중치 표기법
가중치는 층(Layer)의 상태를 나타냅니다. 각 층의 파리마터, 즉 가중치는 최종적으로 모델이 학습을 진행하면서 이 가중치가 변하게 됩니다. 그리고 가중치에 의해 특성들을 더 잘 추출하고 예측을 잘하는 모델이 됩니다.
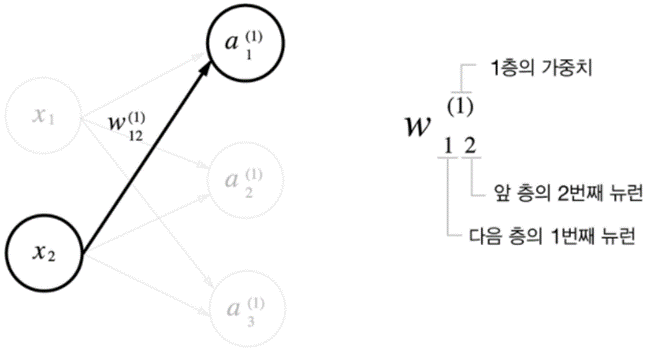
예를 들어, 표기법 W12에 대해 설명드리면, 첫 번째 Layer의 위치한 가중치 요소를 말하며 의미하는 바는 각각 아래와 같습니다.
- 1은 출력 노드 : 출력 레이어(Layer 1)의 첫 번째 노드(ℎ1)
- 2는 입력 노드 : 입력 레이어(Layer 0)의 두 번째 노드(𝑥2)
네트워크 구조 결정 파라미터 설정
하이퍼파라미터는 은닉층(hidden layter) 개수, 노드(뉴런), 활성함수 종류를 선택할 수 있습니다. 얼마나 많은 층을 사용할 것인가? 각 층에 얼마나 많은 노드를 둘 것인가? 이러한 파라미터 값을 변경해 가면서 좋은 모델을 찾는 방법을 사용합니다.
신경망은 하나하나 나눠서 보면 선형 계산식들의 집합입니다. 뉴런의 연결을 하나하나 분리해서 보면 하나의 선형 결합이라는 것을 알 수 있습니다. 선형의 조합이 신경망이라는 비선형을 만든다고 볼 수 있죠. 예를 들어, 하나 뉴런 연결만 보면 h1 = W11 X1 + W12 X2와 같은 선형 수식을 나타낼 수 있습니다.
그렇다면 비선형 연결은 어떻게 만드는 것일까요? 이것이 활성함수가 있어야 하는 이유입니다. 각 노드들이 비선형 변환을 거치지 않으면 아무리 층을 깊게 쌓더라도 효과를 보지 못합니다. 단 하나의 은닉층보다 나은 결과를 내지 못하죠. 신경망 아키텍처 설계에 대해서는 아래 확인해 주시기 바랍니다.
신경망 구조 설계: 딥러닝 아키텍처, Layer(층) 수
신경망 피처 엔지니어링(Feature engineering)
신경망이 자동으로 원본 데이터에서 유용한 특성을 추출하기 때문에 최근 딥러닝은 대부분 특성 공학(feature engineering)이 필요하지 않습니다. 단, 샘플의 개수가 적을 때 좋은 특성을 적은 데이터로 문제를 풀 수 있죠. 이는 적은 자원을 사용하기 때문에 성능도 좋습니다.
특성(feature)의 범위를 비슷하게 맞춰주는 Scaling 작업도 필요합니다. 범주형 데이터에 대해 정수 텐서로 변환하기 위한 원-핫인코딩이라는 방법을 사용합니다.
출력층 설계
신경망은 분류, 회귀 모두에 이용할 수 있습니다. 문론 분류에 많이 사용하기는 합니다. 어떤 문제냐 에 따라 출력층에 사용하는 함수가 달라집니다.
- 회귀 : 항등 함수
- 분류 : 소프트맥스 함수
항등 함수(identity function)
- 입력과 출력이 항상 같다는 뜻에서 항등 함수라고 함
- 출력층에 함등함수를 사용하면 입력 신호가 그대로 출력 신호가 됨(예, 3, 7)
소프트맥스 함수(softmax function)
- 분모는 모든 입력 신호의 지수 함수의 합으로 구성됨
- 소프트맥스 출력은 0 ~ 1 사이의 실수임
- 소프트맥스의 총합은 1 이므로 결과의 확률로 해석할 수 있음(예, 0.2, 0.5 등)
- 신경망 학습시킬 때는 출력층에 소프트맥스 함수를 사용하고 추론 단계에서는 소프트맥스 함수를 생략하는 것이 일반적임(이유는 가장 큰 값으로 결정하면 되기 때문)
'딥러닝' 카테고리의 다른 글
| 활성화 함수 종류: 왜 활성화 함수가 필요할까? (1) | 2024.01.15 |
|---|---|
| 신경망 연산: 딥러닝 가중치 계산 방법 (0) | 2024.01.12 |
| 신경망 구조 설계: 딥러닝 아키텍처, Layer(층) 수 (0) | 2024.01.10 |
| 텐서(Tensor)의 개념: 텐서플로우 vs 파이토치 vs 케라스 (1) | 2024.01.09 |
| RNN(순환 신경망)의 역사: LSTM, seq-to-seq, 트랜스포머 (0) | 2024.01.08 |



